Natürlich sind Frequenzanalysen nichts Neues. Hier stelle ich nur meinen Weg vor, der vielleicht neu ist, auf jeden Fall preisgünstig und eine Möglichkeit für alle diejenigen, die nur einen Computer und das Internet nutzen wollen.

Ich verwende für Frequenzanalysen die Open Source Software Audacity, mit der man nicht nur Frequenzanalysen durchführen kann, sondern auch viele Tonspuren einzeln bespielen könnte, wenn man Musik oder andere Dinge aufnehmen möchte.

Wie mache ich Frequenzanalysen?

Ich starte Audacity, was dann bei mir, mit der Version, die ich nutze, so aussieht:

Sieht doch übersichtlich aus!

Wichtig für Frenquenzanalysen sind nur einige Anklick-Felder.:

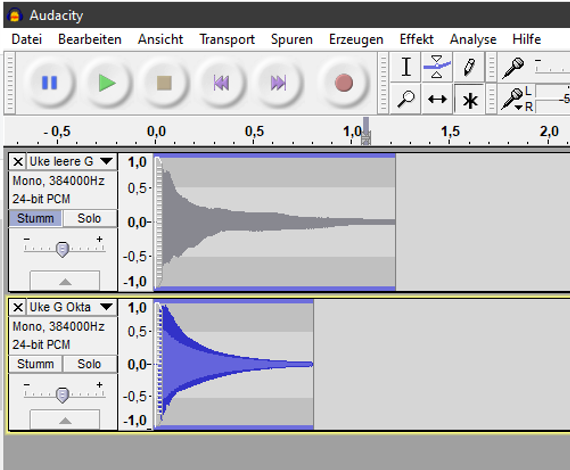
Wenn man oben auf den rote Kreis drückt, wird eine erste Spur angelegt und die Aufnahme beginnt sofort. Ich benutze ein aller einfachstes Mikrophone, nämlich das, was an meinem allerwelts Headset eingebaut ist.

Jede neue Spur heißt erst einmal „Tonspur“. Das Wort kann man anklicken und umbenennen. Bei mir heißt das neue Wort jetzt „Uke leere G-Saite“. Was man außerdem noch sieht, unten blau oben grau, weil ich bei der oberen Spur inzwischen „Stumm“ angeklickt habe, damit die Frequenzen, die ich auf der zweiten Spur aufzeichnen will, sich nicht mit denen überlagern, die aus dem Kopfhörer kommen. Die zweite Spur zeigt nämlich die Aufnahme des Tones, der entsteht, wenn man die gleiche G-Saite im zwölften Bund niederdrückt, also die Oktave von G auf der gleichen Saite spielen möchte.

Man kann die Bilder der Aufnahmen vergrößern, um ein bestimmte Zeitfenster der Aufnahme zu nutzen.

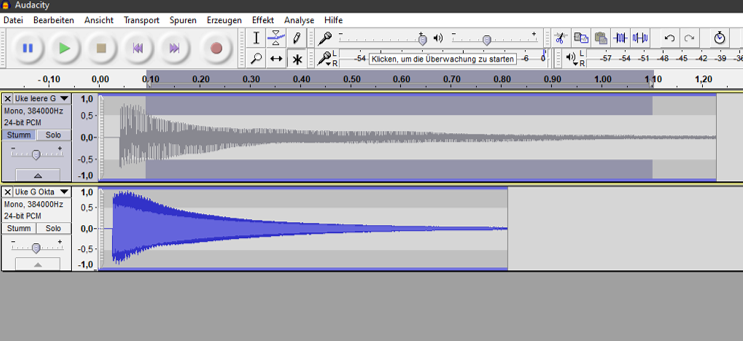
Ich habe hier das eine Sekunde lange Zeitintervall von 0,1 bis 1,1 Sekunden durch Überstreichen mit der Maus gewählt. Ich vermeide die Einschwingzeit in die Analyse einzubeziehen.
Für den so aktivierten Bereich wähle ich aus dem Menü „Analyse“ am oberen Rand des Fensters das Untermenü „Frequenzanalyse“. Das Programm liefert umgehend ein Bild, dass die „Quadratwurzel-Autokorrelationen“ des Tones mit sich selbst zeigt.

Macht nichts! Ich wähle aus den Optionen, die am unteren Rand des neuen Bildes angeboten werden, die Option „Spektrum“.

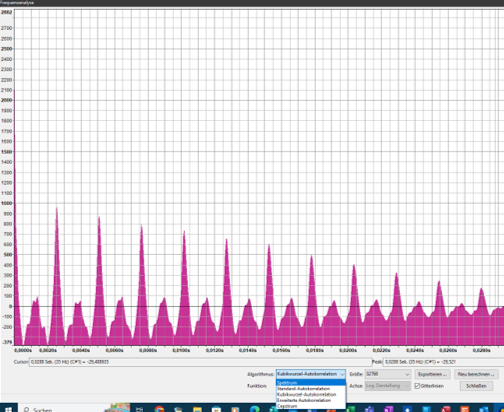
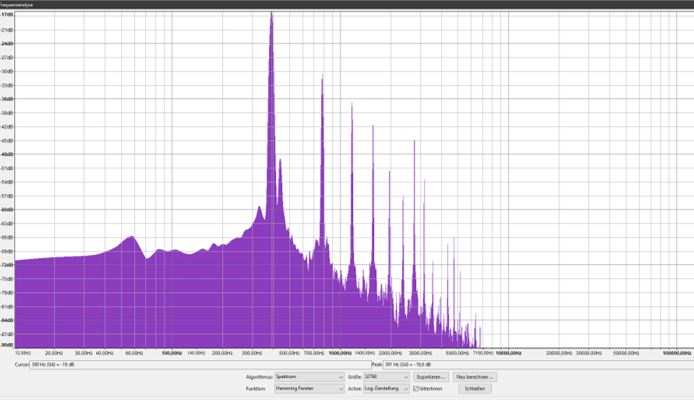
…und erhalte ein Bild, auf dem die verschiedenen Teiltöne des angzupften Tons G4 als „Gipfel“ deutlich herausragen:

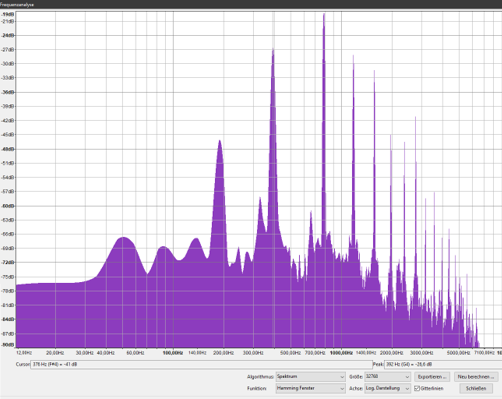
Der erste richtig hohe Peak liegt bei 392 Hz, was man am unteren Rand des Bildes ablesen kann, ebenso wie den Namen des Teil-Tons.

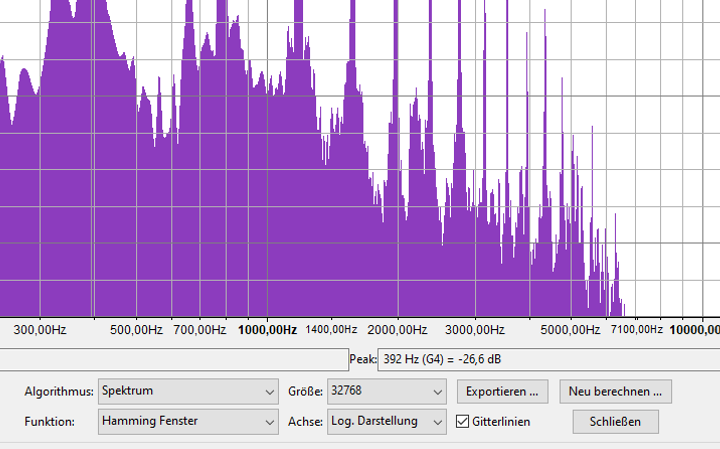
Wenn mann mit der Cusor über das Bild der Frequenzen streicht, dann bleibt er kurz an allen Peaks hängen und zeigt im Feld „Peak“ die Frequenz des Peaks an.

was man im obigen Bild noch sehen Kann: Ich habe eine bestimmte Art der Berechnung der Frequenzen gewählt, nämlich das „Hamming-Fenster“, und die zeitliche Abtastung von 32.768 pro Sekunde.

Die abgelesene Frequenz der Peaks schreibe ich in ein vorbereitetes Excel Rechenblatt.

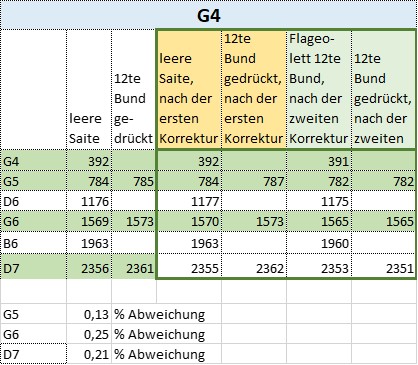
In dem Arbeitsblatt findet man die 392 Hz als einen deutlichen Peak in der Frequenzanalyse des mit der leer angezupften Saite G der Ukulele in der Zeile oben, bei G4. In den folgenden Zellen der Spalte „leere Saite“ findet man die Frequenzen der nächsten deutlichen Peaks.

In der Spalte rechts daneben finden sich die Peak-Frequenzen aus dem im 12ten Bund angezupften Ton. Wie man sieht, gibt es nicht zu allen Teiltönen der in der Spalte „leere Saite“ gefundene Frequenzen gleich Peaks aus dem Ton der Oktave, im 12ten Bund. Vergleicht man aber die gefundenen Teilton-Frequenzen zu G5, G6 und D7 aus den beiden Spalten, dann erhält man die berechneten Frequenzabweichungen in Prozent, die in den unteren drei Zeilen der Tabelle zu finden sind.

Was heißt das nun?

Mein Rechenblatt errechnet , um wieviel mm ich den Auflagepunkt der Saiten auf der Stegeinlage verschieben muss, damit die beiden Töne, der leer angezupfte und der im zwölften Bund gespielte, im Mittel beide ein G sind was man ja gerne möchte…

Bei der Mensur meiner Tenor-Ukulele von 435 mm muss ich den Auflagepunkt auf der Stegeinlage für die G-Saite um 0,43 mm in Richtung des Endklotzes verschieben. Bei einem negativen Vorzeichen müsste ich den Auflagepunkt in Richtung des Griffbretts verschieben. Verschieben heißt hier: mit der Feile eine Fase an die Vordere Kante der Szegeinlage feilen und die Fase polieren, damit die Saite beim Stimmen gut über die Fase rutschen kann und nicht aufgeraspelt wird.

Den ganzen Vorgang führe ich für alle Saiten durch, bei der Gitarre also (mindestens) sechs mal, bei der Ukulele vier mal. Dann kommt der erste Korrektur-Durchgang mit der Feile und anschließend ein zweiter Messdurchgang. Häufig zeigen die zweiten Messungen, dass weitere Korrekturen nötig sind. Ein Beispiel über drei Messungen ist hier im Bereich Intonation zu finden.

Warum messe ich mehrer Peaks aus und bestimme die Abweichung über mehrere Teiltöne?

Das hat mit der „klassischen Testtheorie“ zu tun. Ein Kernsatz darin besagt, dass jeder Messwert aus einem wahren Wert und einem Messfehler besteht. Messfehler bestehen aus systematischen Messfehlern und zufälligen. Den systematischen Messfehler kann man bändigen, indem man Standard-Messbedingungen festlegt, beispielweise sein Gewicht immer vor dem Frühstück erfassen, dann weiß man, dass man eine halbe Stunde ein wenig schwerer ist, aber der Vergleich mit dem Vortagesgewicht ist aussagekräftiger.

Den zufälligen Messfehler kann man mildern, indem man mehrer Messungen des gleichen Merkmals durchführt, die gemessenen Werte addiert und durch die Anzahl der Messwerte dividiert. Das funktionier deshalb, weil zufällige Messfehler „normalverteilt“ um den wahren Wert verteilt liegen, also mal kleiner sind, mal größer als der wahre Wert – eben zufällig.

Bei Gitarren nutze ich bei jeder Saite sechs Teil-Töne, deren einzelne Abweichungen ich summiere und mittele, um näher an den wahren Wert der Abweichung des „Flageolett-Tons über dem zwölften Bund“ von dem „gegriffenen Ton im zwölten Bund“ zu bestimmen.

Bei Ukulelen nutze ich die „leer angezupften Saiten“ und die „gegriffenen Töne im zwölften Bund“, weil die Flageolett-Töne sehr schwach ausgeprägt sind.